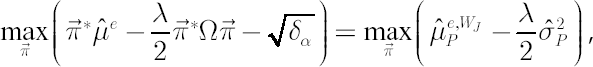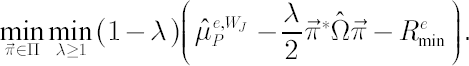Portfolio Optimization
Worst-case scenario optimization
The traditional portfolio optimization framework assumes that parameters of the analytical model are known precisely. In practice, however, statistical estimates of parameters may have significant estimation error. In particular it is relevant for the sample estimate  of vector of vector  that represents the excess part of expected instantaneous rates of return. Ignorance of estimation error in that represents the excess part of expected instantaneous rates of return. Ignorance of estimation error in  usually leads to unwarrantably extreme values of portfolio weights and dramatic shifts in portfolio structure when previous estimates are modified with recent historical data. usually leads to unwarrantably extreme values of portfolio weights and dramatic shifts in portfolio structure when previous estimates are modified with recent historical data.
One way to avoid the mentioned above undesirable properties of an optimal portfolio is to include the estimation error explicitly in optimization process. Most practically sound results in this direction were obtained in [Garlappi, Uppal, Wang; 2005]. The authors implement the following algorithm, which they call Multi-Prior Approach:
- The set
 of possible values for the true vector of possible values for the true vector  is defined. is defined.
- The optimal portfolio, corresponding to relative risk aversion coefficient
 , is obtained by solving the following Min-Max problem: , is obtained by solving the following Min-Max problem:
Note. To consider the robust version of the target shortfall probability criterion the above Min-Max problem must be modified in the following way:
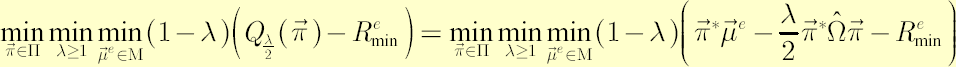
In other words, the investor seeks for portfolio with the best performance under the worst-case scenario. Inner minimization over expected instantaneous excess returns in the above expressions can be regarded as reflection of investor’s uncertainty aversion. A convenient measure for uncertainty aversion degree is confidence level  , used below to define , used below to define  . As . As  approaches 1, investor’s aversion to uncertainty increases to infinity. approaches 1, investor’s aversion to uncertainty increases to infinity.
Two versions of set  are considered below. are considered below.
Separate Confidence Intervals
Let  be the number of portfolio components and be the number of portfolio components and  be sample counterpart of be sample counterpart of  . For every . For every  corresponding confidence interval for corresponding confidence interval for  in the form of in the form of  is obtained by solving the following equation: is obtained by solving the following equation:
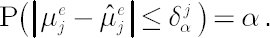
The above equation has the following solution:
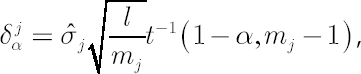
where
 – sample volatility in – sample volatility in  -th asset -th asset
 – average number of observations in one year – average number of observations in one year
 – available number of observations in – available number of observations in  -th asset -th asset
 – inverse function of Student’s t-distribution with – inverse function of Student’s t-distribution with  degrees of freedom: it returns value degrees of freedom: it returns value  such that such that  , where , where  is is 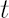 -distributed random variable with -distributed random variable with  degrees of freedom. degrees of freedom.
Set  , corresponding to Separate Confidence Intervals for , corresponding to Separate Confidence Intervals for  , is defined as , is defined as  -dimensional rectangular parallelepiped -dimensional rectangular parallelepiped  . .
Then, the stated Min-Max problem, corresponding to relative risk aversion coefficient  , reduces to , reduces to
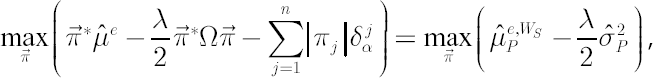
where portfolio worst-case excess Mu  is defined in the following way: is defined in the following way:
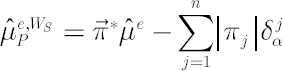
Analogously, the Min-Max problem, corresponding to the target shortfall probability criterion, simplifies to following:
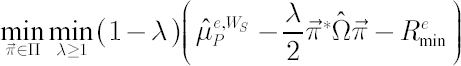
In case of uncorrelated assets the probability of  falling into falling into  is is  . In the general case calculation of the probability of falling into . In the general case calculation of the probability of falling into  is more complicated. It could be desirable to explicitly state the probability of falling into is more complicated. It could be desirable to explicitly state the probability of falling into  than defining it implicitly by means of confidence intervals for individual assets. This is done in the next section. than defining it implicitly by means of confidence intervals for individual assets. This is done in the next section.
Joint Confidence Interval
Suppose all portfolio components possess the same number of observations  . Consider the quantity . Consider the quantity  , which is a sample estimate of squared instantaneous Sharpe ratio for tangency portfolio, corresponding to portfolio excess Mu equal to , which is a sample estimate of squared instantaneous Sharpe ratio for tangency portfolio, corresponding to portfolio excess Mu equal to  . This quantity is a convenient measure for the distance between . This quantity is a convenient measure for the distance between  and and  . .
Joint Confidence Interval  for for  is defined in the following way: is defined in the following way:
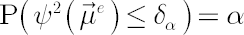
Solution for  has the following form: has the following form:
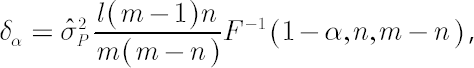
where  is an inverse function of is an inverse function of  -distribution with -distribution with  and and  degrees of freedom: it returns value degrees of freedom: it returns value  such that such that  , where , where  is is  -distributed random variable with -distributed random variable with  and and  degrees of freedom. degrees of freedom.
Set  , corresponding to the above joint confidence interval for , corresponding to the above joint confidence interval for 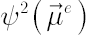 , is defined as follows: , is defined as follows:
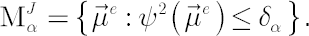
The Min-Max problem, corresponding to risk aversion coefficient  , simplifies to , simplifies to
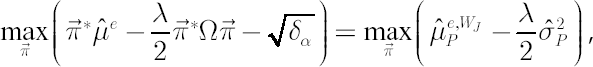
where portfolio worst-case excess Mu 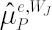 is defined as is defined as 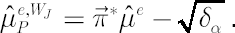
Correspondingly, the Min-Max problem, corresponding to the target shortfall probability criterion, simplifies to the following:
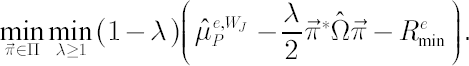
| |
|

 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
portfolio optimization
\
robust optimization
The Theory
\
Details
\
portfolio optimization
\
robust optimization







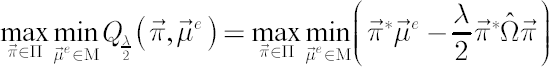
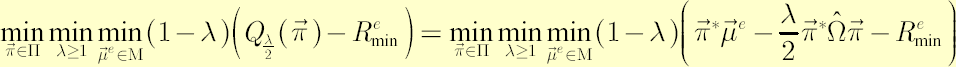
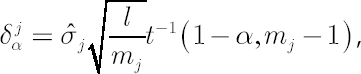
 .
.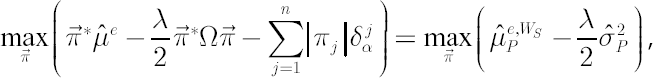
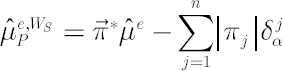
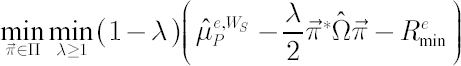
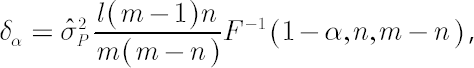
 is
is