Portfolio Analytics
Analytical portfolio
Dynamics of Portfolio Wealth, generated by Portfolio Strategy with Constant Weights
Assume that discounted prices of assets  move according to the analytical model with Mu vector move according to the analytical model with Mu vector  , vector of continuously compounded dividend yields , vector of continuously compounded dividend yields 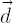 , covariance matrix , covariance matrix  and risk-free rate and risk-free rate  . For . For
simplicity assume that the vector  is constant through time. Then dynamics of discounted portfolio wealth is constant through time. Then dynamics of discounted portfolio wealth  , corresponding to portfolio vector , corresponding to portfolio vector  , satisfies the , satisfies the
following equation:
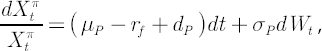
where
 is a Wiener process, is a Wiener process,

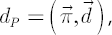

Note. Readers who are not familiar with stochastic differential equations in continuous time may interpret 
as very short time range,  as a simple return on portfolio over as a simple return on portfolio over  and and  as a normally as a normally
distributed random variable with zero mean and variance  , independent of other variables , independent of other variables  , ,
 . .
Definition. Quantity  is called Portfolio Mu, or Portfolio Expected Instantaneous Simple Rate of Return. is called Portfolio Mu, or Portfolio Expected Instantaneous Simple Rate of Return.
Definition. Quantity  is called Portfolio Dividend Yield. is called Portfolio Dividend Yield.
Definition. Quantity  is called Portfolio Excess Mu. is called Portfolio Excess Mu.
Definition. Quantity  is called Portfolio Volatility. is called Portfolio Volatility.
Definition. Quantity  is called Portfolio Expected Excess Growth Rate. is called Portfolio Expected Excess Growth Rate.
The latter definition reflects the easily derived equality  . .
Decomposition of Portfolio Variance
The direct consequence of the portfolio volatility definition is the following decomposition of portfolio variance  : :

where  . Obviously, . Obviously, 
Element  denotes proportion of portfolio variance, contributed by denotes proportion of portfolio variance, contributed by  -th asset. -th asset.
In other words, vector  with components, called Contributions to Portfolio Risk, determines alternative representation of portfolio structure, measured in units of portfolio variance rather than wealth, as in case of vector with components, called Contributions to Portfolio Risk, determines alternative representation of portfolio structure, measured in units of portfolio variance rather than wealth, as in case of vector  . .
| |
|

 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
portfolio analytics
\
analytical portfolio
The Theory
\
Details
\
portfolio analytics
\
analytical portfolio








 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
portfolio analytics
\
analytical portfolio
The Theory
\
Details
\
portfolio analytics
\
analytical portfolio