Portfolio Optimization
Utility functions approach vs. mean-variance approach
Assume that the analytical model holds in the market with 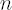 assets, excess Mu vector assets, excess Mu vector 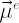 and the covariance matrix and the covariance matrix 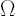 . By . By 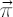 we denote the vector of constant portfolio weights. we denote the vector of constant portfolio weights.
Mean-Variance Approach can be formulated in several equivalent ways.
- Minimization of portfolio volatility subject to the lower constraint on portfolio excess Mu (over all admissible portfolios
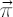 ): ):
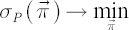 subject to subject to 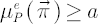
- Maximization of portfolio Excess Mu subject to the upper constraint on portfolio volatility (over all admissible portfolios
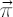 ): ):
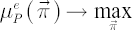 subject to subject to 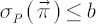 , where , where 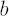 is a strictly positive constant. is a strictly positive constant.
- Maximization of the following expression (over all admissible portfolios
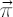 ): ):
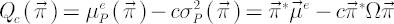 , where , where 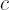 is a strictly positive constant. is a strictly positive constant.
Utility Function Approach consists in maximizing the expected value 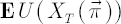 of utility function of utility function 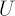 from portfolio terminal wealth from portfolio terminal wealth 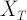 over all admissible portfolios over all admissible portfolios 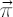 . .
Key Result
Under the assumptions of the analytical model the maximization of expected CRRA utility with the relative risk aversion coefficient  from terminal wealth and the maximization of from terminal wealth and the maximization of 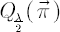 (both maximizations are taken over all admissible portfolio vectors (both maximizations are taken over all admissible portfolio vectors 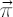 ) result in the same optimal portfolio ) result in the same optimal portfolio 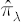 . .
Important! The above statement allows all the results obtained in single-period framework to be easily extended to multi-period one with CRRA Utility Functions.
Note. 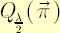 is also known as the Risk-Adjusted Expected Excess Rate of Return, corresponding to the relative risk aversion coefficient is also known as the Risk-Adjusted Expected Excess Rate of Return, corresponding to the relative risk aversion coefficient 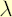 . .
| |

 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
portfolio optimization
\
mean-variance criterion
The Theory
\
Details
\
portfolio optimization
\
mean-variance criterion








 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
portfolio optimization
\
mean-variance criterion
The Theory
\
Details
\
portfolio optimization
\
mean-variance criterion