Dynamic portfolio strategies
Proportional Transaction Costs and Inaction Region
Transactions in the financial market are often accompanied by essential costs. As a rule, an investor comes across the transaction costs proportional to the total volume of transactions made. Such costs are more often adhered to the value of bid-ask spread and the broker commissions. Alternative kind of costs, also investigated in literature, are called fixed costs. Fixed costs do not depend on the volume of the transaction.
Below we shall concentrate on the proportional transaction costs. The portfolio strategy which consists in continuous maintenance of given portfolio weights in such a situation appears unacceptable. Indeed, as the turnover of such strategy can be very high, the associated transaction costs arising during portfolio rebalancing also becomes unreasonably high.
The qualitative form of theoretically optimal strategy in the presence of proportional transaction costs is illustrated below by the examples of portfolios which consist of one and two risky assets.
One Asset Example
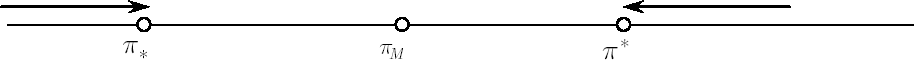
Let 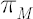 be the optimal weight in risky asset in absence of transaction costs (the only component of the Merton portfolio). Let be the optimal weight in risky asset in absence of transaction costs (the only component of the Merton portfolio). Let 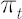 denote current weight in risky asset at time denote current weight in risky asset at time 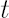 . .
The optimal strategy in presence of transaction costs is described by the following rules:
- Appropriate critical weights
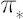 and and 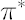 such that such that 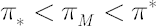 are calculated. are calculated.
- While
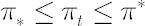 , no transactions take place. , no transactions take place.
- Once
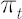 reaches reaches 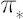 , investor must transact the minimal amount required to keep , investor must transact the minimal amount required to keep 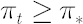 . .
- Once
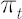 reaches reaches 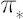 , investor must transact the minimal amount required to keep , investor must transact the minimal amount required to keep 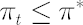 . .
In other words, 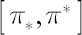 defines the inaction region, and portfolio weight defines the inaction region, and portfolio weight 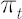 is constantly kept inside this region once (due to price fluctuations) is constantly kept inside this region once (due to price fluctuations) 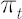 is driven to one of its borders. is driven to one of its borders.
General Case
When there is more then one risky asset in portfolio, the situation becomes far more complicated, but the logic of the optimal behavior essentially stays the same.
- There exists the so-called inaction region (coherent set, situated in
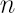 -dimensional space of portfolio weights), where no transactions take place while portfolio weights belong to the above set. -dimensional space of portfolio weights), where no transactions take place while portfolio weights belong to the above set.
- Immediately after the portfolio vector abandons the inaction region, an investor must transact the minimal amount in appropriate assets, which is required to keep portfolio weights from leaving the inaction region. In other words, the inaction region frontier plays role of reflecting boundary.
Note. As a rule, point in 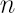 -dimensional space, defined by the Merton portfolio, lies inside the inaction region. The latter point is called the Merton point. -dimensional space, defined by the Merton portfolio, lies inside the inaction region. The latter point is called the Merton point.
Two Assets Example
Lets apply the above 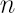 -dimensional optimal rule to two-dimensional case of portfolio assets -dimensional optimal rule to two-dimensional case of portfolio assets 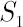 and and 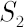 . .
The picture below shows the inaction region with Merton point 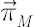 inside it. All possible types of transactions that are required to send portfolio weights back to the inaction region are shown with arrows. inside it. All possible types of transactions that are required to send portfolio weights back to the inaction region are shown with arrows.
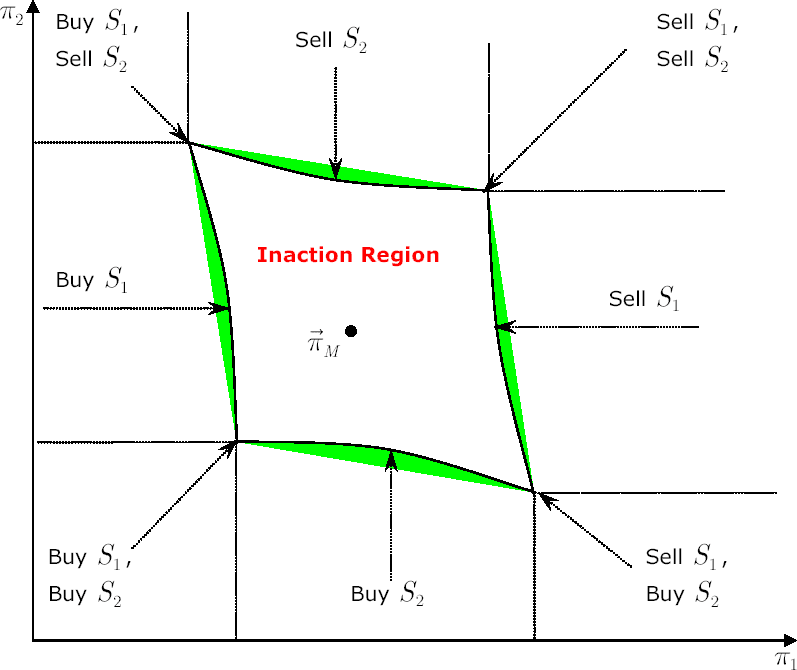
Calculating the Inaction Region
It follows from the above that optimal portfolio strategy under proportional transaction costs is completely defined by its inaction region. Unfortunately, it seems that the obstacles arising when the attempts are made to find analytical solution for the exact form of inaction region are insurmountable.
There are many publications devoted to the problem of finding the reasonable approximation for the inaction region, most of which contain some numerical procedures (see, for example, [Muthuraman, Kumar;
2006]). On the contrary, we will focus on the result first obtained in[Davis, Norman; 1990] and extended to the multidimensional case by D. Kramkov and S. Volkov in 1996.1 In special settings they managed to find a closed analytical solution for the inaction region approximation, which works quite satisfactory in practice.
Assumptions of the Model
- The authors work in the framework of the analytical model, modified to include proportional transaction costs, represented by vector
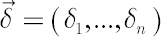 , where , where 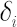 denotes the costs size in the denotes the costs size in the 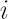 -th -th
asset. For example, 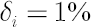 means that means that 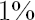 of the total amount traded in the of the total amount traded in the 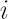 -th asset is contributed to costs. Usually -th asset is contributed to costs. Usually 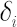 is close to the Bid-Ask Spread, expressed in % of the asset price. is close to the Bid-Ask Spread, expressed in % of the asset price.
- The CRRA utility functions, determined by relative risk aversion coefficient
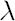 , are considered. , are considered.
- All possible structures of the inaction region are restricted to cuboids (rectangular parallelepipeds in
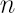 -dimensional space) with the Merton point in the center. -dimensional space) with the Merton point in the center.
Note. The specified shapes of the inaction region contain the optimal one only when all portfolio assets are uncorrelated. But there are two reasons why their use is justified. On the one hand, portfolio
strategies with cuboid region of inaction are significantly easier to implement. On the other hand, practical benefits received from utilizing cuboid region of inaction and from inaction regions of more
sophisticated shapes are insignificant.
- Since obtained results are expressed in asymptotic form, their usage is limited to sufficiently small transaction costs (around 5% or less).
Formulas for the inaction region
Let 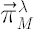 denote denote 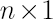 -vector, corresponding to the Merton portfolio with relative risk aversion -vector, corresponding to the Merton portfolio with relative risk aversion 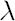 . .
Define an Inaction Region  in the following way: in the following way:
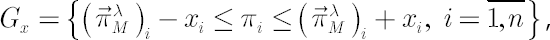
where 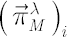 , , 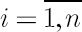
, correspond to 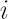 -th component of Merton portfolio. -th component of Merton portfolio.
Denote the following vectors and matrices:
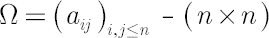 -covariance matrix -covariance matrix
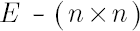 -identity matrix -identity matrix
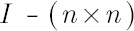 -matrix of ones -matrix of ones
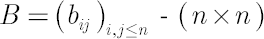 -matrix, defined by the following equality: -matrix, defined by the following equality:
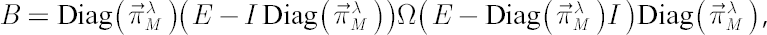
where 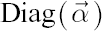 denotes a diagonal matrix with elements of denotes a diagonal matrix with elements of 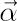 at the main diagonal. Also denote at the main diagonal. Also denote
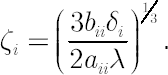
Let 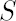 -set denote such a set that is symmetrical relative to all coordinate axes, translated to the Merton point. -set denote such a set that is symmetrical relative to all coordinate axes, translated to the Merton point.
Key Result
Vector 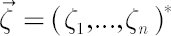 , defined above, determines the inaction region , defined above, determines the inaction region 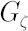 , which is asymptotically (for , which is asymptotically (for 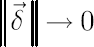 optimal among all optimal among all 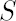 -sets. Obtained order of asymptotic convergence is -sets. Obtained order of asymptotic convergence is 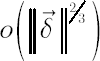 . .
1 To our knowledge, no results of theirs were published in English-speaking journals.
| |
|

 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
dynamic strategies
\
transaction costs and inaction region
The Theory
\
Details
\
dynamic strategies
\
transaction costs and inaction region







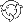
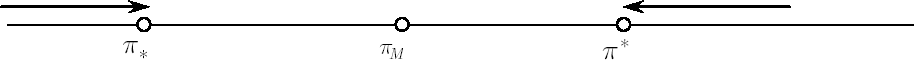

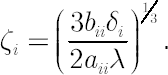
 .
.