Factor-based Asset Pricing Models
Capital Asset Pricing model
Capital Asset Pricing Model (CAPM) is virtually a one-factor asset pricing model with market portfolio as its only factor. The most common choice for market portfolio is broad market index such as S&P 500 for U.S. Stock Market.
The assumptions underlying CAPM extensively use notions of an efficient market and “rational” investor, who invests in market portfolio and riskless asset only. Under this assumptions a market equilibrium is achieved, that leads to the CAPM framework.
One of CAPM consequences is well-known CAPM equation. This equation sets relationship between assets excess Mu and their sensitivities to market portfolio, called Beta (for further notations look in Factor-based Asset Pricing Models):
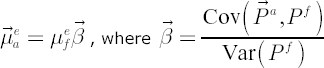
Essential CAPM advantage is its simplicity, which admits graphical illustration.
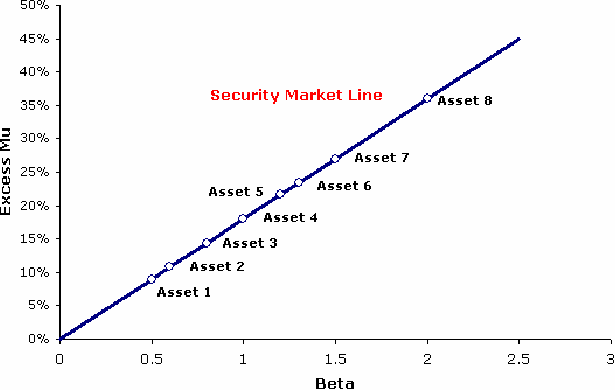
Straight line with slope  that relates assets betas and their respective excess Mu values is called Security Market Line (SML). that relates assets betas and their respective excess Mu values is called Security Market Line (SML).
Portfolio Beta
Beta of portfolio  is calculated as a linear combination of individual betas: is calculated as a linear combination of individual betas:

As expected, point  also belongs to SML: also belongs to SML: 
Portfolio Variance
Under the CAPM assumptions portfolio variance  admits the following decomposition: admits the following decomposition:
 , where , where  denotes variance of the market portfolio. denotes variance of the market portfolio.
As before, the first item on the right side of the above expression is called portfolio systematic risk, while second one is called portfolio diversifiable risk.
| |

 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
asset-pricing models
\
CAPM
The Theory
\
Details
\
asset-pricing models
\
CAPM







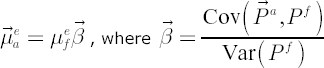


 , where
, where