Model Parameters Estimation
Advanced estimates
Stambaugh combined-sample estimates for means and covariances
This technique consists in obtaining maximum-likelihood estimates of the model parameters for assets with different start dates and common final date.
In the event of portfolio components having different depths of historical data standard parameters estimates, considered in the previous section, result in a loss of information. The covariance matrix of portfolio components, calculated based on a historical dataset with different start dates is not necessarily positive-definite. Hence, the analyzed dataset is truncated traditionally to the date corresponding to the asset with the shortest history. With such an approach, the loss of the information contained in the initial dataset set is inevitable.
The method suggested in [Stambaugh; 1997], consists in the consecutive use of the regression of assets with a shorter history on assets with a longer history. This time all the information contained in the data is used.
Note. It is worth mentioning that the use of the entire dataset improves estimates for longer-history assets as well as estimates for shorter-history assets.
For more detailed information on the discussed method see [Stambaugh; 1997].
About shrinkage estimators
The shrinkage estimator is a statistical tradeoff between the bias and the estimation error. For the first time the shrinkage estimator appeared in [Stein; 1956], where it was shown that “shrinking” sample means of multivariate normal distribution to an appropriate common constant improves estimation accuracy.
In general, the shrinkage estimate is obtained via a “shrinkage” of sample unbiased estimate towards some biased target with lower estimation error.
Shrinking sample excess Mu towards excess Mu of GMV portfolio
Shrinking sample covariance matrix towards constant correlations covariance matrix
Shrinking sample estimates towards values, implied by asset pricing model
Shrinking sample excess Mu towards excess Mu of GMV portfolio
Shrinkage estimator for 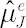 was obtained in [Jorion; 1986]. Based on Bayes approach, estimate was obtained in [Jorion; 1986]. Based on Bayes approach, estimate 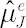 implies shrinking os sample Mu implies shrinking os sample Mu 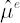 towards a common constant, equal to sample excess Mu towards a common constant, equal to sample excess Mu 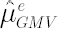 for global minimum variance portfolio. Calculation formulae for for global minimum variance portfolio. Calculation formulae for 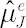 are presented below: are presented below:
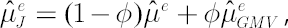
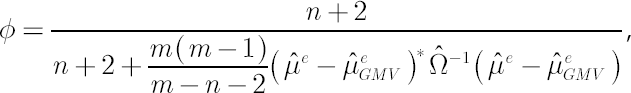
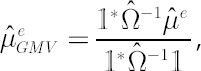
where 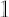 is is 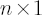 vector of ones; vector of ones;
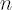 is number of assets; is number of assets;
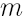 is number of observations. is number of observations.
Shrinking sample covariance matrix towards constant correlations covariance matrix
This estimate is a shrinkage estimator for covariance matrix. It was proposed in [Ledoit, Wolf; 2004].
Final estimate 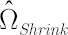 is obtained via shrinkage of the sample covariance matrix towards the covariance matrix, produced by averaging correlations across asset pairs. is obtained via shrinkage of the sample covariance matrix towards the covariance matrix, produced by averaging correlations across asset pairs.
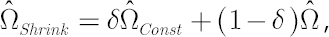
where
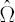 – sample covariance matrix, – sample covariance matrix,
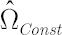 – constant correlations covariance matrix. – constant correlations covariance matrix.
Details, including the formulas for the optimal shrinkage intensity 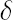 can be found in [Ledoit, Wolf; 2004]. can be found in [Ledoit, Wolf; 2004].
Shrinking sample estimates towards values, implied by asset pricing model
The given method of the estimation of parameters 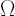 and and 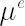 , first suggested in [Pastor, Stambaugh; 1999], consist in applying Bayes approach, which assumes a certain degree of investor's confidence in that the market satisfies the selected factor-based asset pricing model (such as CAPM or Fama-French 3-factor model). , first suggested in [Pastor, Stambaugh; 1999], consist in applying Bayes approach, which assumes a certain degree of investor's confidence in that the market satisfies the selected factor-based asset pricing model (such as CAPM or Fama-French 3-factor model).
The degree of investor’s confidence in the chosen factor model is determined by the parameter 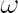 , taking values in the range form 0 to 1. Value , taking values in the range form 0 to 1. Value 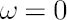 means that the investor completely ignores predictions of the factor model, using as estimates for means that the investor completely ignores predictions of the factor model, using as estimates for  and and 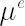 their sample counterparts, while their sample counterparts, while 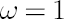 means, that the estimates for means, that the estimates for 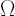 and and 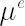 coincide with model-implied estimates coincide with model-implied estimates 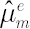 and and  . .
Analytical formulas in general case 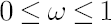 are presented in [Wang; 2005]. are presented in [Wang; 2005].
Joint estimator for means and covariances based on Missing Factor approach
This method described in [MacKinlay, Pastor; 2000] can be applied in a situation when there are reasons to believe that the dynamics of the portfolio assets is determined by influence of one factor only, however the factor itself is "unobservable", i.e. the structure of the latter is unknown.
Note. By an unobservable factor one may imply the unknown structure of the market portfolio.
Let vector 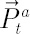 denote simple rates of return for assets on the interval denote simple rates of return for assets on the interval 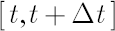 , where , where 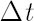 is small enough. By is small enough. By 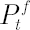 we shall designate corresponding simple rate of return of an unobserved factor. we shall designate corresponding simple rate of return of an unobserved factor.
Suppose that the dynamics of the portfolio components satisfies the one-factor model
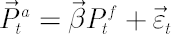
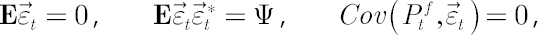
where 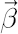 denotes vector of betas and vector denotes vector of betas and vector 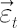 contains regression residuals. contains regression residuals.
The additional assumption made in [MacKinlay, Pastor; 2000] is that the covariance’s matrix of the residuals 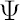 is proportional to the identity matrix: is proportional to the identity matrix:
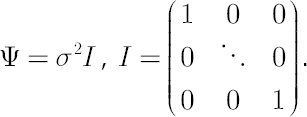
The above assumption, basically, is not burdensome if portfolio components belong to the same asset class (big-cap stocks, small-cap stocks, bonds etc.).
With the assumptions made it is possible to establish a connection between a covariance matrix 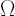 and a vector and a vector 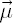 , as a result one obtains estimates , as a result one obtains estimates 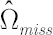 and and 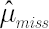 . Analytical formulas used in calculation of . Analytical formulas used in calculation of 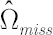 and and 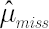 are given in [Kan, Zhou, 2005]. are given in [Kan, Zhou, 2005].
| |
|

 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
parameters estimation
\
advanced estimates
The Theory
\
Details
\
parameters estimation
\
advanced estimates








 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
parameters estimation
\
advanced estimates
The Theory
\
Details
\
parameters estimation
\
advanced estimates